I’m posting here a link to an interview that I did awhile back for the Spanish newspaper El Pais (a few people have been asking me about it). The interview was a conversation with journalist Daniel Mediavilla, who originally contacted me to gain a bit more insight into the Tiny Blue Dot funded project that we are carrying out designing numadelic VR experiences to help alleviate anxiety in patients that are facing life-threatening illnesses. The result in a far-ranging discussion on several topics including fear of death, psychedelics, scientific reductionism, quantum mechanics, the relation between scientific enquiry and spiritual enquiry…

The interview is available in both Spanish and also in English.

I’ve been having a lot of fun over the last 18 months re-discovering my guitar, playing, and singing… I’ve even been writing songs & making recordings, some of which I’ve posted on my soundcloud account. A few of these songs formed the basis for a live performance I gave at Oxford University in November 2024, at an event entitled “The Museum of Consciousness” curated by Karl H Smith.

I’m super happy to announce that we have received news of support from the Tiny Blue Dot Foundation for development of our numadelic XR work! Specifically, we received support for a project entitled “Numadelic VR Experiences for Improving Mental Health Outcomes in Patients Facing Life-Threatening Illness”.

This project will enable us to develop a set of group numadelic XR experiences called Clear Light that can support those who have recently received terminal diagnoses like cancer. Clear Light will enable people to reimagine themselves as energetic (rather than material) essences. In so doing, Clear Light will offer people a new perspective on death – not as an end to be feared, but rather as a change of state which they can approach with a sense of peace, curiosity, and acceptance. It is an amazing privilege to have support to carry out this work.

I’m writing a paper about my near-death experience, which is what has underpinned a lot of my aesthetic over these last years. This video illustrates how I perceived my body – as a pulsing light. The light intensity grew with each inhale, and diminished with each exhale. Overall, the amplitude envelope was decreasing. I knew that at the moment it was extinguished, I would begin resting. In another dimension. It seems it wasn’t the time.

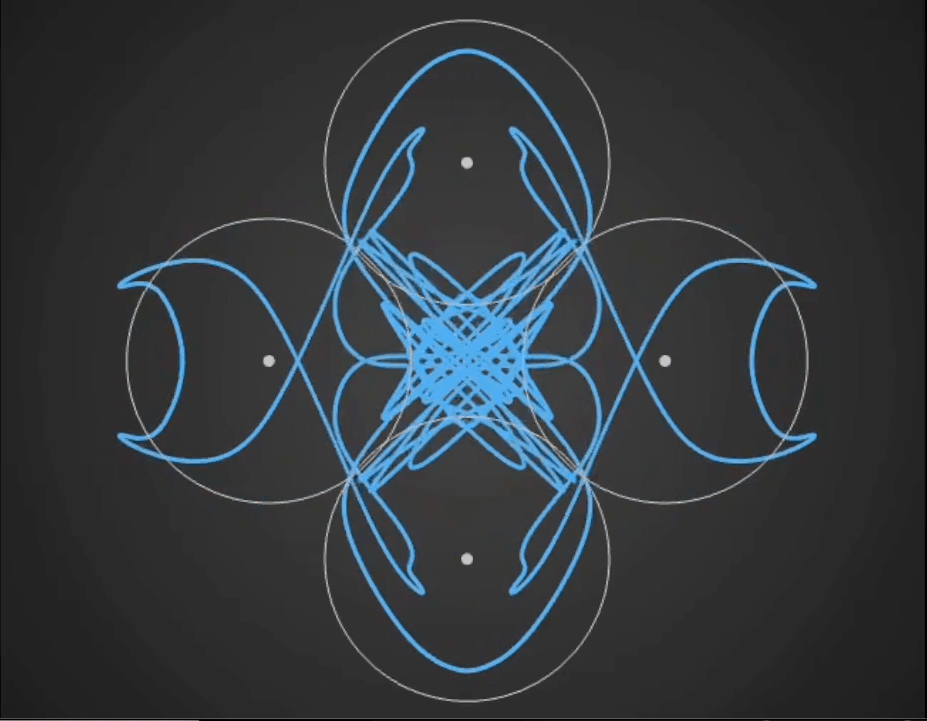
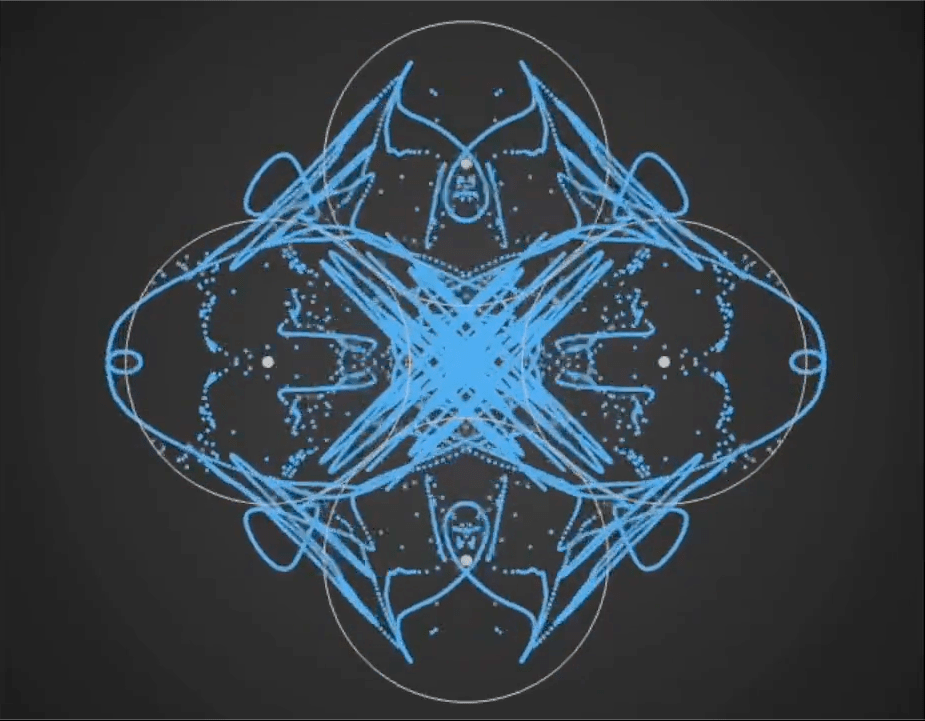
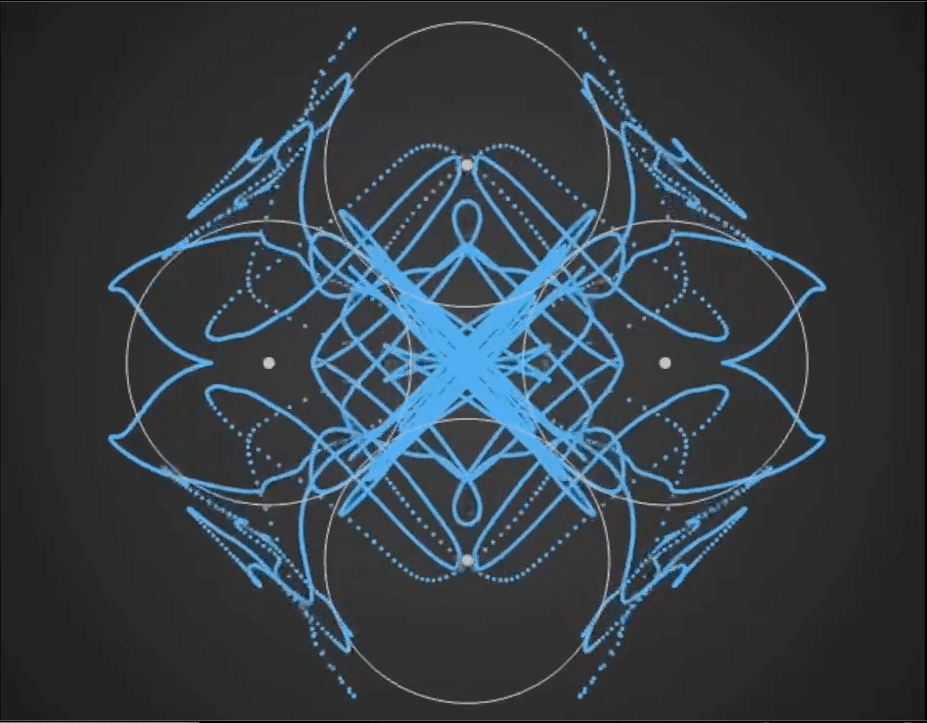
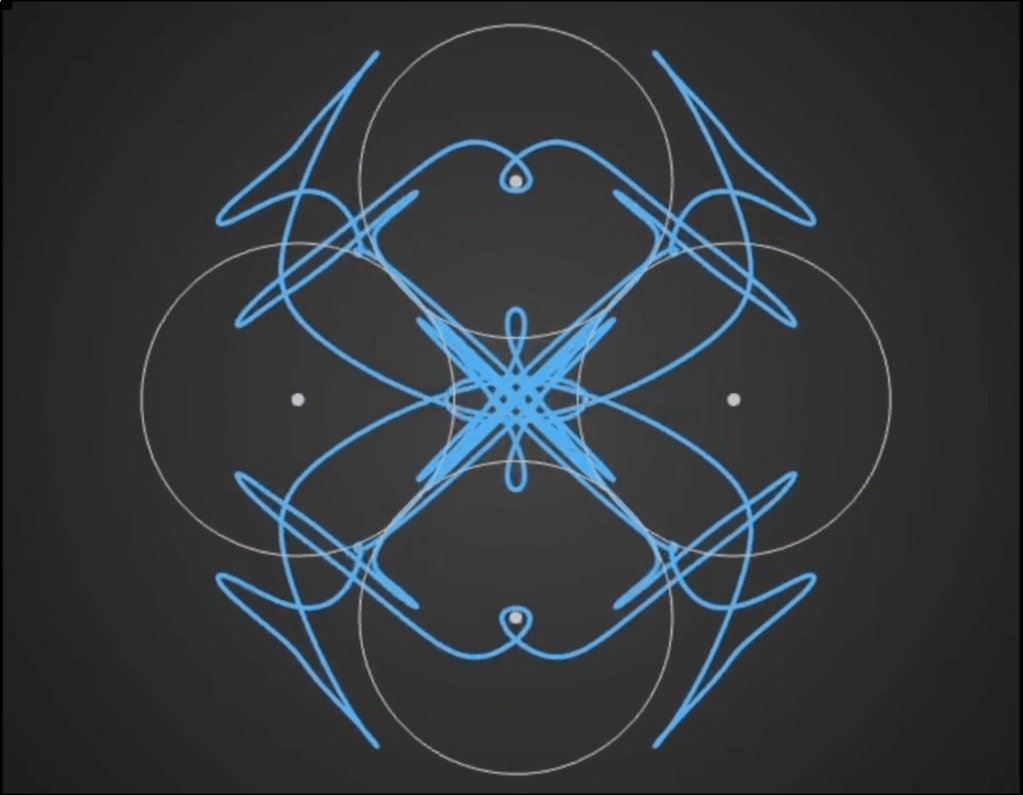
Here’s a demo video from ‘Gaussian Fields’, a new physics art C++ real-time simulation code I have been working on. It’s a generative framework, so you never know exactly what patterns will emerge once you set the dynamics in motion. It’s cool to see intricate and varied complexity evolve from such simple initial conditions….

Intangible Realities Laboratory (IRL) headquarters has moved to the CiTIUS | Centro Singular de Investigación en Tecnoloxías Intelixentes in Santiago de Compostela. To celebrate the incarnation of IRL 2.0, we have a shiny new website!

www.intangiblerealitieslab.org

To read more, check out the article “Group VR experiences can produce ego attenuation and connectedness comparable to psychedelics” available open access at www.nature.com/articles/s41598-022-12637-z

Green Tara in progress… Tārā is a buddha manifestation embodying the qualities of feminine energy within the universe. She offers warmth, compassion, and relief from suffering. Like a mother for her children, she engenders, nourishes, and smiles at the vitality of creation. In her Green form, Tārā offers protection from the variety of unfortunate circumstances encountered by beings trapped in cyclic existence. She is characterized by wind energy, enabling her to act quickly to ease the suffering of her children.